Magnetic Field from a Wire Lab
This is a physics simulation that calculates and visualizes the magnetic field strength generated in the around a current-carrying wire using the Biot-Savart Law. The simulation allows users to adjust the current in the wire and the distance of the magnetic field sensor from the wire to observe the effect on the magnetic field strength.
Usage:
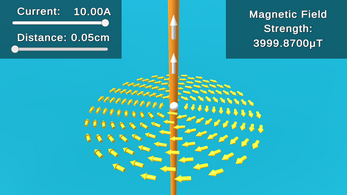
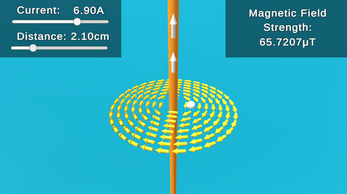
- Fill in the input fields with current (in amperes) and distance (in centimeters) of the sensor from the wire, then observe the magnetic field strength (in microtesla) and the direction of the magnetic field
- Look at the yellow arrows (magnetic field lines) to visualize the strength and direction of the magnetic field
- The white sphere represents the magnetic field sensor, and the two white arrows represent the direction of conventional current
- The orange cylinder represents the current-carrying wire
Definitions:
- Current-carrying wire: A conductor, usually a metal wire, through which an electric current flows
- Magnetic field (B): A vector field that surrounds magnets and electric currents, exerting a force on charged particles and other magnetic materials, measured in the SI unit of tesla (T) or microtesla (μT) which is 1/1,000,000th of a tesla
- Biot-Savart Law: A fundamental equation in electromagnetism that describes the magnetic field generated by a steady electric current, particularly for an infinitely long current-carrying wire
- Current (I): Flow of electric charge through a conductor, measured in amperes (A)
- Distance (r): Distance between the current-carrying wire and the magnetic field sensor, measured in centimeters (cm)
Formula:
B = (μ₀ * I) / (2 * π * r)
Where μ₀ is the magnetic constant, also known as the permeability of free space, which is 4π × 10^-7 T·m/A, I is the current in amperes, and r is the distance from the wire in meters (converted from centimeters by dividing by 100).
| Status | Released |
| Platforms | HTML5 |
| Author | riyadwritescode |
| Genre | Simulation |
| Made with | Unity |
| Tags | 3D, Indie, Physics, Unity |

Leave a comment
Log in with itch.io to leave a comment.